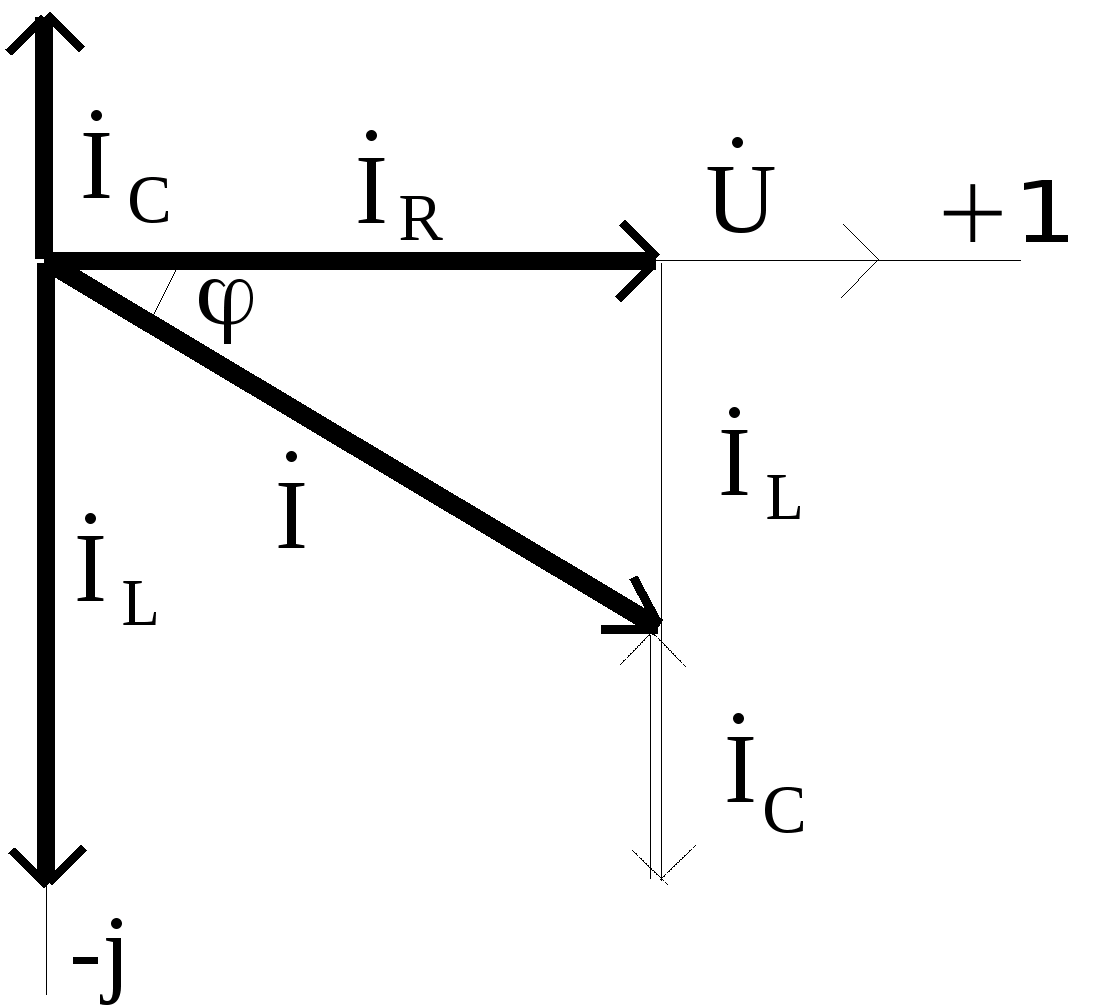а) Понятие о векторах
На рис. 1-4 приведена кривая изменения переменного тока во времени. Ток сначала растет от нуля (при = 0°) до максимального положительного значения + I M (при = 90°), затем убывает, переходит через нуль (при = 180°), достигает максимального отрицательного значения — I M (при = 270°) и, наконец, возвращается к нулю (при = 360°). После этого весь цикл изменения тока повторяется.
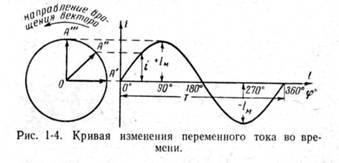

Кривая изменения переменного тока во времени, построенная на рис. 1-4, называется синусоидой. Время Т, в течение которого происходит полный цикл изменения тока, соответствующий изменению угла до 360°, называется периодом переменного тока. Число периодов за 1 с называется частотой переменного тока. В промышленных установках и в быту в СССР и в других странах Европы используется главным образом переменный ток частотой 50 Гц. Этот ток 50 раз в секунду принимает положительное и отри цательное направление.
Изменение переменного тока во времени можно записать в следующем виде:
где i — мгновенное значение тока, т. е. значение тока в каждый момент времени; I м — максимальное значение тока; — угловая частота переменного тока, f= 50 Гц, = 314; — начальный угол, соответствующий моменту времени, с которого начинается отсчет времени (при t = 0).
Для частного случая, показанного на рис. 1-4,
Анализируя действие устройств релейной защиты и автоматики, необходимо сопоставлять токи и напряжения, складывать или вычитать их, определять углы между ними и производить другие операции. Пользоваться при этом кривыми, подобными приведенной на рис. 1-4, неудобно, поскольку построение синусоид тока и напряжения занимает много времени и не дает простого и наглядного результата. Поэтому для упрощения принято изображать токи и напряжения в виде отрезков прямых линий, имеющих определенную длину и направление, — так называемых векторов (ОА на рис. 1-4). Один конец вектора закреплен в точке О — начало координат, а второй вращается против часовой стрелки.
Мгновенное значение тока или напряжения в каждый момент времени определяется проекцией на вертикальную ось вектора, длина которого равна максимальному значению электрической величины тока или напряжения. Эта проекция будет становиться то положительной, то отрицательной, принимая максимальные значения при вертикальном расположении вектора.
За время Т, равное периоду переменного тока, вектор совершит полный оборот по окружности (360°), занимая последовательно положения и т. д. При частоте переменного тока 50 Гц вектор будет совершать 50 об/с.
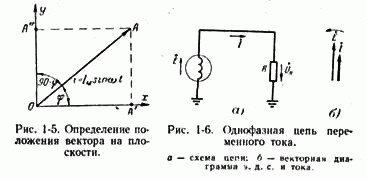
Таким образом, вектор тока или напряжения — это отрезок прямой, равный по величине максимальному значению тока или напряжения, вращающийся относительно точки О против движения часовой стрелки со скоростью, определяемой частотой переменного тока. Зная положение вектора в каждый момент времени, можно определить мгновенное значение тока или напряжения в данный момент. Так, для положения вектора тока ОА, показанного на рис. 1-5, его мгновенное значение определяется проекцией на вертикальную ось, т. е.
На основании рис. 1-5 можно также сказать, что ток в данный момент времени имеет положительную величину. Однако это еще не дает полного представления о протекании процесса в цепи переменного тока, так как неизвестно, что значит положительный или отрицательный ток, положительное или отрицательное напряжение.
Для того чтобы векторные диаграммы токов и напряжений давали полную картину, их нужно увязать с фактическим протеканием процесса в цепи переменного тока, т. е. необходимо предварительно принять условные положительные направления токов и напряжений в рассматриваемой схеме.

Без выполнения этого условия, если не заданы положительные направления токов и напряжений, любая векторная диаграмма не имеет никакого смысла.
Рассмотрим простую однофазную цепь переменного тока, приведенную на рис. 1-6, а. От однофазного генератора энергия передается в активное сопротивление нагрузки R. Зададимся положительными направлениями токов и напряжений в рассматриваемой цепи.
За условное положительное направление напряжения и э д. с. примем направление, когда потенциал вывода генератора или нагрузки, связанного с линией, выше потенциала вывода, соединенного с землей. В соответствии с правилами, принятыми в электротехнике, положительное направление для э. д. с. обозначено стрелкой, направленной в сторону более высокого потенциала (от земли к линейному выводу), а для напряжения — стрелкой, направленной в сторону более низкого потенциала (от линейного вывода к земле).
Построим векторы э. д. с. и тока, характеризующие работу рассматриваемой цепи (рис. 1-6, б). Вектор э. д. с. произвольно обозначим вертикальной линией со стрелкой, направленной вверх. Для построения вектора тока запишем для цепи уравнение согласно второму закону Кирхгофа:
Поскольку знаки векторов тока и э. д. с. в выражении (1-7) совпадают, вектор тока будет совпадать с вектором э. д. с. и на рис. 1-6, б.

Здесь и в дальнейшем при построении векторов будем откладывать их по величине равными эффективному значению тока и напряжения, что удобно для выполнения различных математических операций с векторами. Как известно, эффективные значения тока и напряжения в раз меньше соответствующих максимальных (амплитудных) значений.
При заданных положительных направлениях тока и напряжения однозначно определяется и знак мощности. Положительной в рассматриваемом случае будет считаться мощность, направленная от шин генератора в линию:
так как векторы тока и э. д. с. на рис. 1-6, б совпадают.
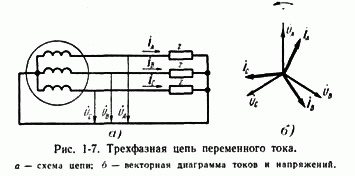
Аналогичные соображения могут быть высказаны и для трехфазной цепи переменного тока, показанной па рис. 1-7,а.
В этом случае во всех фазах приняты одинаковые положительные направления, чему соответствует симметричная диаграмма токов и напряжений, приведенная на рис. 1-7, б. Отметим, что симметричной называется такая трехфазная система векторов, когда все три вектора равны но величине и сдвинуты относительно друг друга на угол 120°.
Вообще говоря, совсем не обязательно принимать одинаковые положительные направления во всех фазах. Однако принимать разные положительные направления в разных фазах неудобно, так как пришлось бы изображать несимметричную систему векторов при работе электрической цепи в нормальном симметричном режиме, когда все три фазы находятся в одинаковых условиях.
б) Операции с векторами
Когда мы рассматриваем только одну кривую тока или напряжения, начальное значение угла, с которого начинается отсчет или, иначе говоря, положение вектора на диаграмме, соответствующее начальному моменту времени, может быть принято произвольным. Если же одновременно рассматриваются два или несколько токов и напряжений, то, задавшись начальным положением на диаграмме одного из векторов, мы тем самым уже определяем положение всех других векторов.
Все три вектора фазных напряжений показанные на рис. 1-7, б, вращаются против часовой стрелки с одинаковой скоростью, определяемой частотой переменного тока. При этом они пересекают вертикальную ось, совпадающую с направлением вектора на рис. 1-7,б, поочередно с определенной последовательностью, а именно которая называется чередованием фаз напряжения (или тока).
Для того чтобы определить взаимное расположение двух векторов, обычно говорят, что один из них опережает или отстает от другого. При этом опережающим считается вектор, который при вращении против часовой стрелки раньше пересечет вертикальную ось. Так, например, можно сказать, что вектор напряжения на рис. 1-7, б опережает на угол 120°, или, с другой стороны, вектор отстает от вектора на угол 120°. Как видно из рис. 1-7, выражение «вектор отстает на угол 120°» равноценно выражению «вектор опережает на угол 240°».
При анализе разных электрических схем возникает необходимость складывать или вычитать векторы тока и напряжения. Сложение векторов производится геометрическим суммированием по правилу параллелограмма, как показано на рис. 1-8, а, на котором построена сумма токов
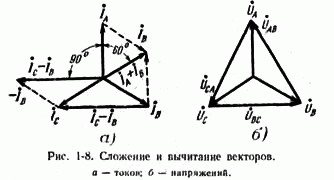

Так как вычитание — действие обратное сложению, очевидно, что для определения разности токов (например, достаточно к току прибавить вектор, обратный
Вместе с тем на рис. 1-8, а показано, что вектор разности токов можно построить проще, соединив линией концы векторов При этом стрелка вектора разности токов направлена в сторону первого вектора, т. е.
Совершенно аналогично строится векторная диаграмма междуфазных напряжений, например (рис. 1-8, б).
Очевидно, что положение вектора на плоскости определяется его проекциями на две любые оси. Так, например, для того чтобы определить положение вектора ОА (рис. 1-9), достаточно знать его проекции на взаимно перпендикулярные оси
Отложим на осях координат проекции вектора и и восстановим из точек перпендикуляры к осям. Точка пересечения этих перпендикуляров и есть точка А — один конец вектора, вторым концом которого является точка О — начало координат.
в) Назначение векторных диаграмм
Работникам, занимающимся проектированием и эксплуатацией релейной защиты, весьма часто приходится использовать в своей работе так называемые векторные диаграммы — векторы токов и напряжений, построенные на плоскости в определенном сочетании, соответствующем электрическим процессам, происходящим в рассматриваемой схеме.
Векторные диаграммы токов и напряжений строятся при расчете коротких замыканий, при анализе токораспре-деления в нормальном режиме.
Анализ векторных диаграмм токов и напряжений является одним из основных, а в ряде случаев единственным способом проверки правильности соединения цепей тока и напряжения и включения реле в схемах дифференциальных и направленных защит.
По сути дела, построение векторной диаграммы целесообразно во всех случаях, когда к рассматриваемому реле подаются две или больше электрических величин: разность токов в максимальной токовой или дифференциальной защите, ток и напряжение в реле направления мощности или в направленном реле сопротивления. Векторная диаграмма позволяет сделать заключение о том, как рассматриваемая защита будет работать при коротком замыкании, т. е. оценить правильность ее включения. Взаимное расположение векторов токов и напряжений на диаграмме определяется характеристикой рассматриваемой цепи, а также условно принятыми положительными направлениями токов и напряжений.
Для примера рассмотрим две векторные диаграммы.
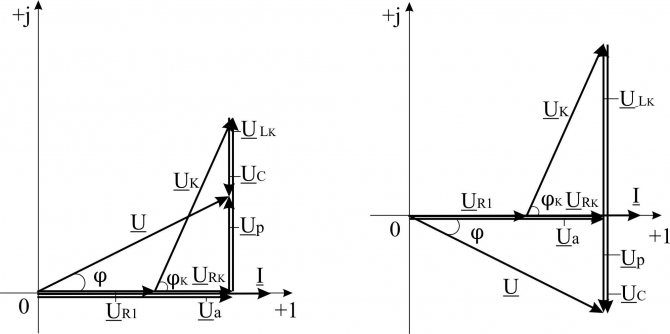
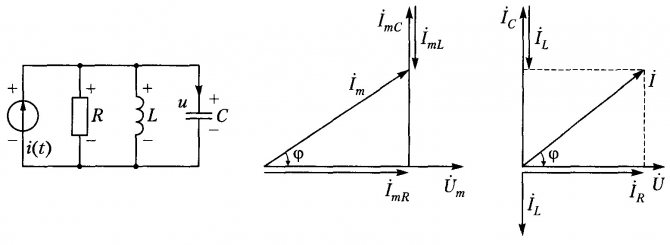
На рис. 1-10, а показана однофазная цепь переменного тока, состоящая из генератора и последовательно соединенных емкостного активного и индуктивного сопротивлений (примем, что индуктивное сопротивление больше емкостного x L > x C). Положительные направления токов и напряжений, так же как и в случаях, рассмотренных выше, обозначены на рис. 1-10, а стрелками. Построение векторной диаграммы начнем с вектора э. д. с, который расположим на рис. 1-10, б вертикально. Величина тока, проходящего в рассматриваемой цепи, определится из следующего выражения:
Поскольку в рассматриваемой цепи имеются активные и реактивные сопротивления, причем x L > x C , вектор тока отстает от вектора напряжения на угол :
На рис. 1-10, б построен вектор отстающий от вектора на угол 90°. Напряжение в точке n определяется разностью векторов . Напряжение в точке m определится аналогично:
г) Векторные диаграммы при наличии трансформации
При наличии в электрической цепи трансформаторов необходимо ввести дополнительные условия, для того чтобы сопоставлять векторные диаграммы токов и напряжений на разных сторонах трансформатора. Положительные направления токов при этом следует задавать с учетом полярности обмоток трансформатора.
В зависимости от направления намотки обмоток трансформатора взаимное направление токов в них меняется. Для того чтобы определять направление токов в обмотках силового трансформатора и сопоставлять их между собой, обмоткам трансформатора дают условные обозначения «начало» и «конец».
Нарисуем схему, приведенную на рис. 1-6, только между источником э. д. с. и нагрузкой включим трансформатор (рис. 1-12, а). Обозначим начала обмоток силового трансформатора буквами А и а, концы — X и х. При этом следует иметь в виду, что «начало» одной из обмоток принимается произвольно, а второй — определяется на основании условных положительных направлений токов, заданных для обеих обмоток трансформатора.На рис. 1-12, а указаны положительные направления токов в обмотках силовых трансформаторов. В первичной обмотке положительным считается направление тока от «начала» к «концу», а во вторичной — от «конца» к «началу».
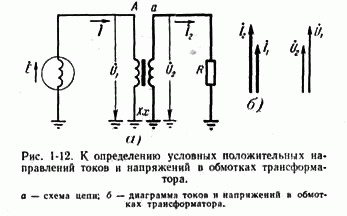

В результате при таких положительных направлениях направление тока в сопротивлении нагрузки остается таким же, что и до включения трансформатора (см. рис. 1-6 и 1-12).
где — магнитные потоки в магнитопроводс трансформатора, а — создающие эти потоки намагничивающие силы (н. с).
Из последнего уравнения
Согласно равенству (1-11) векторы имеют одинаковые знаки и, следовательно, будут совпадать по направлению (рис. 1-12, б).
Принятые положительные направления токов в обмотках трансформатора удобны тем, что векторы первичного и
Вторичного токов на векторной диаграмме совпадают по направлению (рис. 1-12, б). Для напряжений также удобно принять такие положительные направления, чтобы векторы вторичного и первичного напряжений совпадали, как показано на рис. 1-12.
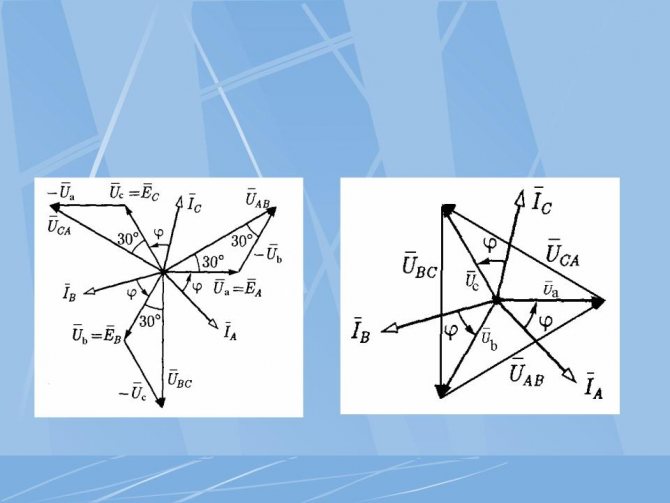
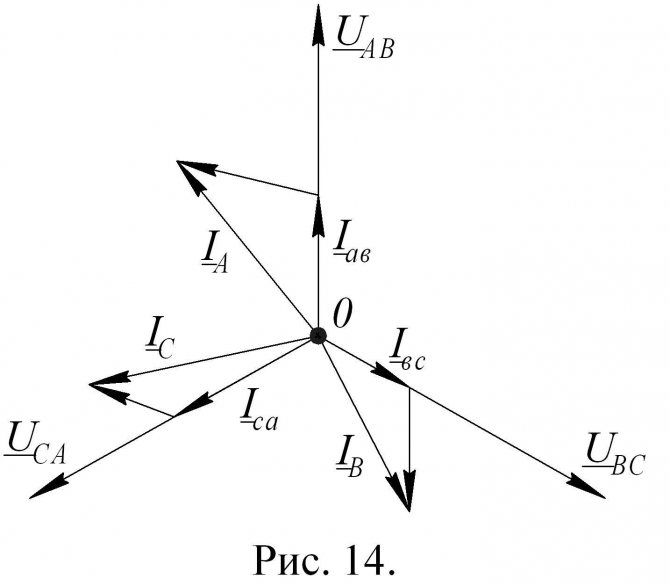
В рассматриваемом случае имеет место соединение трансформатора по схеме 1/1-12. Соответственно для трехфазного трансформатора схема соединений и векторная диаграмма токов и напряжений показаны на рис. 1-14.
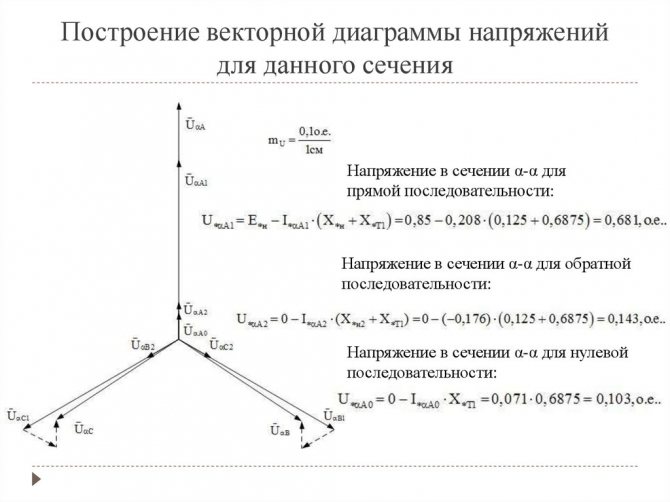
На рис. 1-15, б построены векторные диаграммы напряжений, соответствующие схеме соединения трансформатора
![]()
![]()
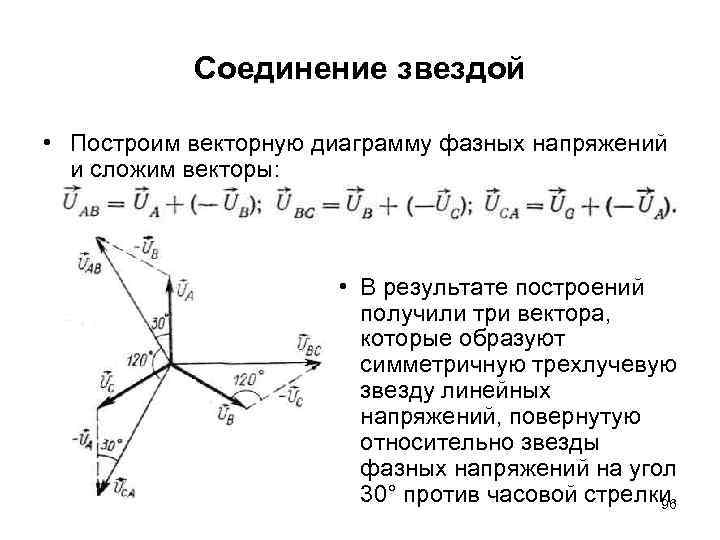
На стороне высшего напряжения, где обмотки соединены в звезду, междуфазные напряжения в раз превышают фазные напряжения. На стороне же низшего напряжения, где обмотки соединены в треугольник, междуфазные и фазные напряжения равны. Междуфазные напряжения стороны низшего напряжения отстают на 30° от аналогичных междуфазных напряжений стороны высшего напряжения, что и соответствует схеме соединений
Для рассматриваемой схемы соединений обмоток трансформатора можно построить и векторные диаграммы токов, проходящих с обеих его сторон. При этом следует иметь в виду, что на основании принятых нами условий определяются только положительные направления токов в обмотках трансформатора. Положительные же направления токов в линейных проводах, соединяющих выводы обмоток низшего напряжения трансформатора с шинами, могут быть приняты произвольно независимо от положительных направлений токов, проходящих в треугольнике.
Так, например, если принять положительные направления токов в фазах на стороне низшего напряжения от выводов, соединенных в треугольник, к шинам (рис. 1-15, а), можно записать следующие равенства:
Соответствующая векторная диаграмма токов показана на рис. 1-15, в.
Аналогично можно построить векторную диаграмму токов и для случая, когда положительные направления токов приняты от шин к выводам треугольника (рис. 1-16, а). Этому случаю соответствуют следующие равенства:
и векторные диаграммы, приведенные на рис. 1-16, б. Сравнивая диаграммы токов, приведенные на рис. 1-15, в и 1-16, б, можно сделать вывод, что векторы фазных токов, проходящих в проводах, соединяющих выводы обмоток низ-
Шего напряжения трансформатора и шины, находятся в про-тивофазе. Конечно, как те, так и другие диаграммы верны.
Таким образом, при наличии в схеме обмоток, соединенных в треугольник, необходимо задаваться положительными направлениями токов как в самих обмотках, так и в линейных проводах, соединяющих треугольник с шинами.
В рассматриваемом случае при определении группы соединений силового трансформатора удобно за положительные принимать направления от выводов низшего напряжения к шинам, так как при этом векторные диаграммы токов совпадают с принятым обозначением групп соединения силовых трансформаторов (сравните рис. 1-15, б и в). Аналогично могут быть построены векторные диаграммы токов и для других групп соединения силовых трансформаторов. Сформулированные выше правила построения векторных диаграмм токов и напряжений в схемах с трансформаторами действительны и для измерительных трансформаторов тока и напряжения.
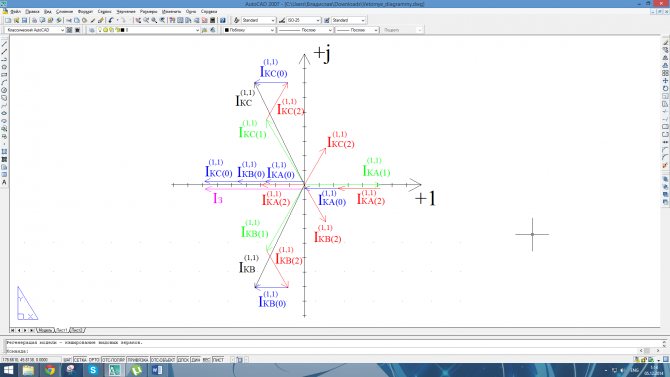
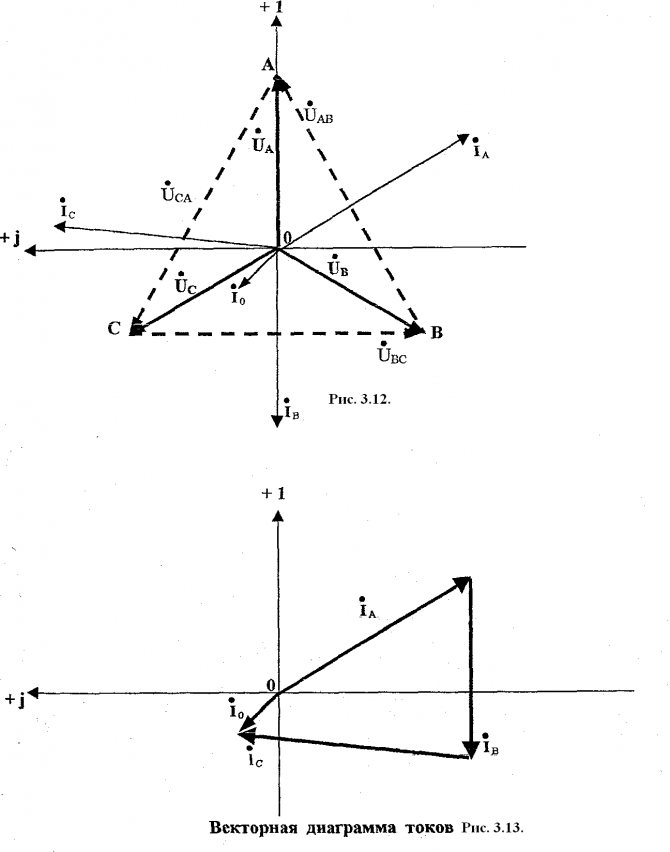
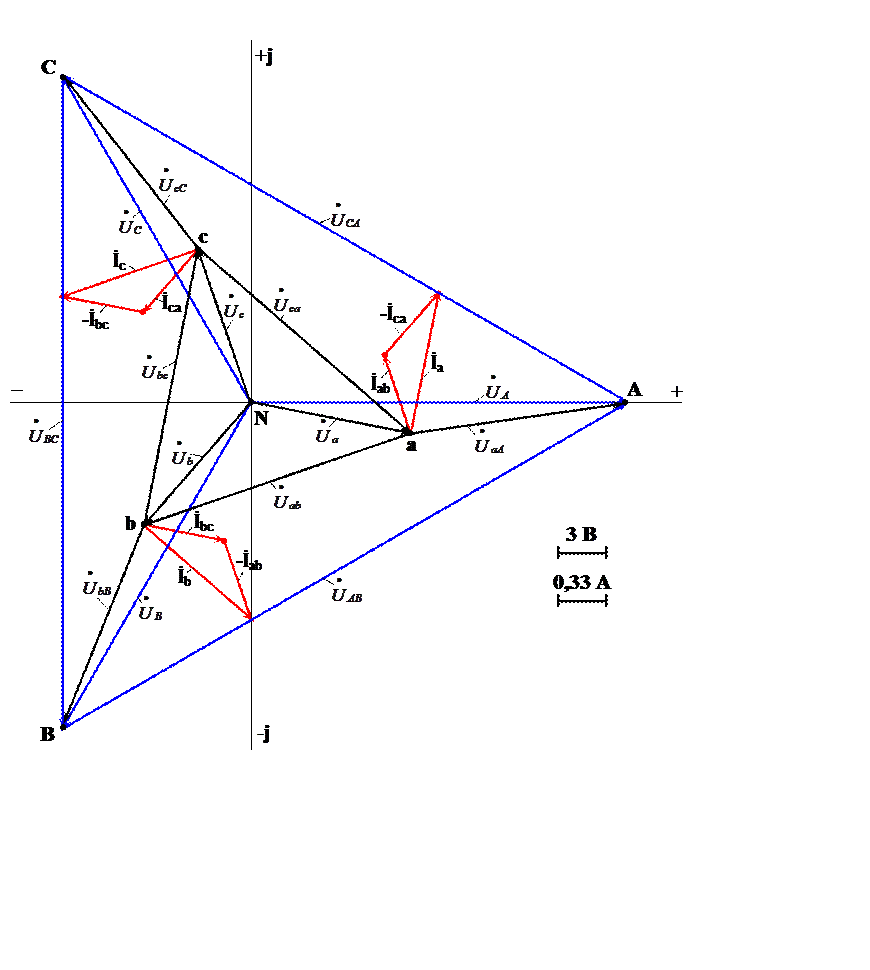
Рассмотрен для случая с исправным нулевым проводом. Векторные диаграммы напряжений и токов даны на рисунках 15 и 16; на рисунке 17 дана совмещенная диаграмма токов и напряжений
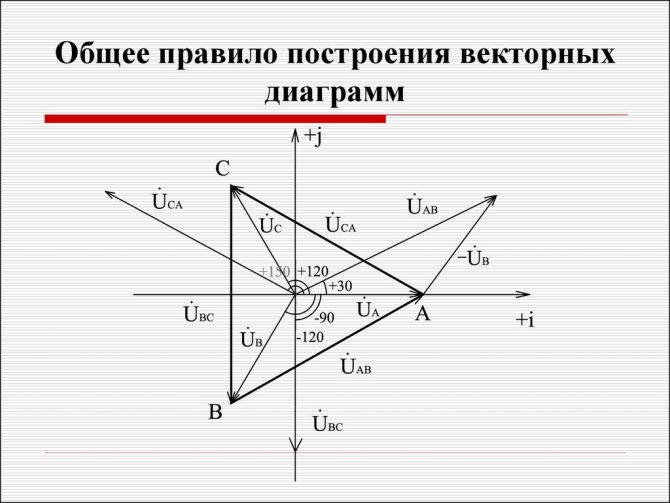
1. Строятся оси комплексной плоскости: действительных величин (+1) — горизонтально, мнимых величин (j) — вертикально.
2. Исходя из значений модулей токов и напряжений и размеров полей листов, отведеных для построения диаграмм, выбираются масштабы тока mI и напряжения mU. При использовании формата А4 (размеры 210х297 мм) при наибольших модулях (см. табл. 

тока 54 А и напряжения 433 В приняты масштабы: mI = 5 А/см, mU = 50 В/см.
3. С учетом принятых масштабов mI и mU определяется длина каждого вектора, если диаграмма строится с использованием показательной формы его записи; при использовании алгебраической формы находятся длины проекций векторов на оси действительных и мнимых величин, т.е. длины действительной и мнимой частей комплекса.
Например, для фазы А:
Длина вектора тока / ф.А / = 34,8 А/ 5 А/см = 6,96 см; длина его действительной части
I ф.А = 30 А/ 5 А/см = 6 см,
длина его мнимой части
I ф.А = -17,8 А/5 А/см = — 3,56 см;
Длина вектора напряжения / А нагр./ = 348 В/ 50 В/см = 6,96 см; длина его действительной части
U А нагр. = 340,5 В/ 50 В/см = 6,8 см;
длина его мнимой части
U Анагр. = 37,75 В/ 50 В/см = 0,76 см.
Результаты определения длин векторов, их действительных и мнимых частей отражены в таблице 9.
Таблица 9 — Длины векторов тока и напряжения, их действительных и мнимых частей для случая неповрежденного нулевого провода.
| Величина | Масштаб, 1/см | Длина вектора, см | Длина действительной части, см | Длина мнимой части, см | |
| Напряжения фаз сети | U А | 50 В/см | 7,6 | 7,6 | |
| UВ | 7,6 | — 3,8 | — 6,56 | ||
| UС | 7,6 | — 3,8 | 6,56 | ||
| Напряжения фаз нагрузки | U Анагр. | 50 В/см | 6,96 | 6,8 | 0,76 |
| UВ нагр. | 7,4 | — 4,59 | — 5,8 | ||
| UС нагр. | 8,66 | -4,59 | 7,32 | ||
| U0 | 1,08 | 0,79 | — 0,76 |
Продолжение таблицы 9
| Токи фаз нагрузки | I ф.А | 5 А/см | 6,96 | 6.0 | — 3,56 |
| I ф.В | 7,4 | 1,87 | — 7,14 | ||
| I ф.С | 3,13 | 0,1 | 3,12 | ||
| I 0 | 10,8 | 7,9 | — 7,6 |
Как сделать лучевую векторную диаграмму связей в Excel
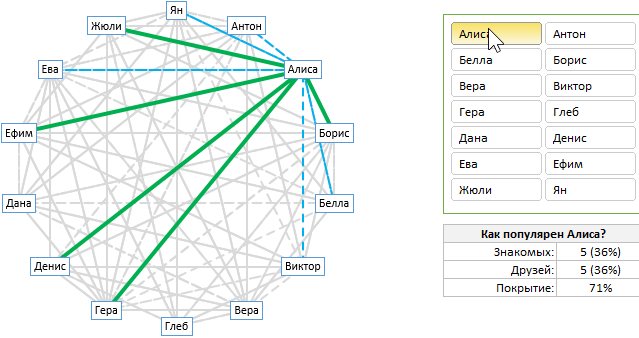

Сначала взглянем на то, что мы пытаемся построить и визуально оценим объем работы. Выглядит интересно? Тогда читайте дальше, чтобы узнать, как это создать.
Чтобы создать лучевую диаграмму в Excel для визуального анализа взаимоотношений в сети, нам нужно сначала понять ее различные составляющие.
Как видите, диаграмма содержит следующие части:
- Набор точек, каждая из которых представляет одну заинтересованную сторону – участники сети.
- Набор сероватых толстых сплошных и тонких пунктирных линий, представляющих все отношения между людьми. Сплошные – сильные связи (например, друзья), пунктирные – слабые связи (знакомые).
- Набор зеленых толстых и синих пунктирных линий, представляющих отношения для выбранного конкретного участника сетевой группы.
- Срез для выбора анализа участника – как панель управления лучевой диаграммой.
- Табличка со сводной статистикой выбранного человека.
Порядок построения диаграмм
Таким образом, с помощью векторных диаграмм, возможно очень четко представить себе опережение или отставание, затрагивающее различные электрические величины. В качестве примера можно рассмотреть ток, у которого величина изменяется по определенному закону: i = Im sin (ω t + φ).
Для построения диаграммы необходимо от начальной точки координат «0» под определенным углом φ провести вектор Im. Его величина будет соответствовать такому же току. Направление вектора следует выбирать таким образом, чтобы он составлял угол с осью ОХ, равный фазе φ. Проекция вектора на вертикальной оси даст значение мгновенного тока в первоначальный период времени.
В большинстве случаев на векторных диаграммах отображаются не амплитудные, а действующие значения. Отличие действующих и амплитудных значений представляет собой пропорцию в определенном масштабе: I = Im /√2. Таким образом, векторная диаграмма напряжений и токов дает возможность быстро и просто выполнять все необходимые действия с двумя основными параметрами при расчетах электрических цепей и получать точные результаты.
Умножитель напряжения
Расчет делителя напряжения
В чем измеряется напряжение
Как проверить напряжение мультиметром в сети: измерение вольтажа в розетке 220 вольт
Индикатор напряжения на светодиодах: схема, как сделать своими руками самодельный указатель напряжения в сети
Расчет тока по мощности и напряжению
Задание базового вектора для векторной диаграммы
Перейти к содержимому
FaultAn.ru
Просто РЗА
- Интерактив Расчёт электрических цепей Доступ к программе
- Инструкция по расчёту
- Отзывы
- Использование просмотрщика осциллограмм
- Построение векторных диаграмм
- Анализ спектра сигнала
- Использование фильтра Фурье
- ТОЭ
- Осциллограммы
- Контакты
FaultAn.ru
Просто РЗА
Показать/Скрыть навигацию
Показать/Скрыть навигацию
- Интерактив Расчёт электрических цепей Доступ к программе
- Инструкция по расчёту
- Отзывы
- Использование просмотрщика осциллограмм
- Построение векторных диаграмм
- Анализ спектра сигнала
- Использование фильтра Фурье
Разновидности векторных диаграмм
Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.
С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.
Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.
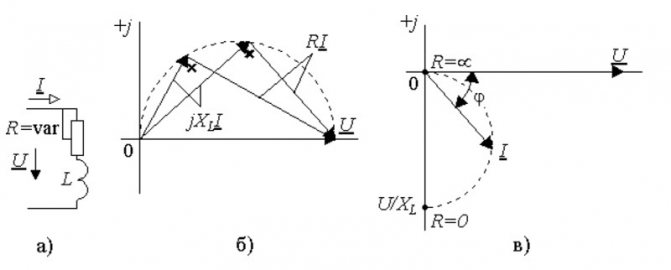

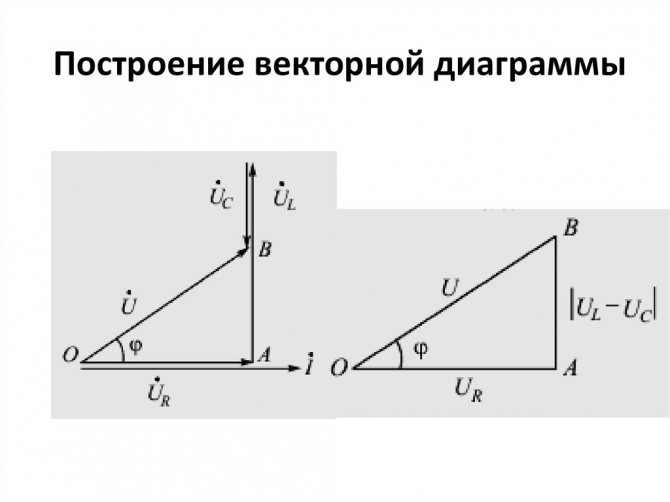
Круговая диаграмма
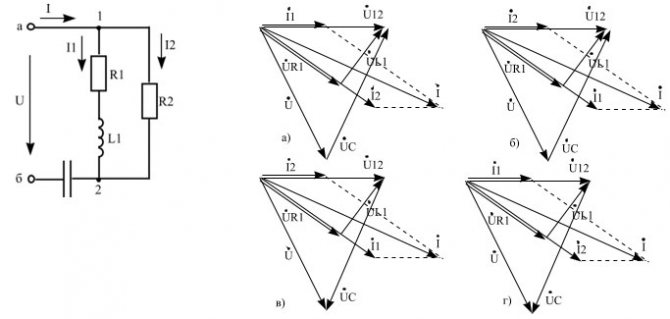
Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.
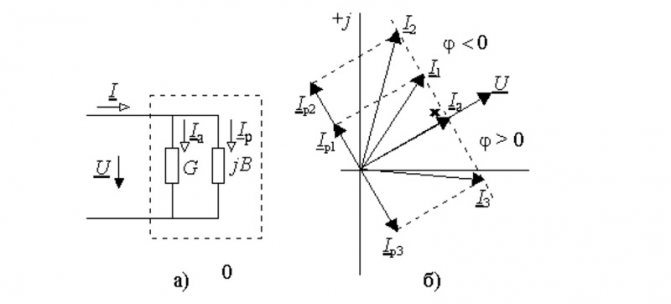
Линейная диаграмма
Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.
Разновидности
Разобравшись, что такое и для чего применяется векторная диаграмма, нужно узнать какие разновидности построения существуют. Они отличаются по характеру построения и типу. По характеру бывают:
- Точными. Векторная точная диаграмма — это отображение выполненного численного расчета в соответствующем масштабе. С помощью нее определяют параметры фаз и амплитудные значения строго геометрическим способом.
- Качественные. Такие гистограммы строят для наблюдения взаимосвязи между электровеличинами без использования числовых характеристик. Такой способ позволяет экспериментировать с различными параметрами и моделировать процессы в электроцепях.
Векторную диаграмму токов можно построить 2 разными способами:
- Круговым. В ее принципе лежит вектор, который описывает изменение характеристик путем образования круга или полукруга на плоскости. При таком варианте учитывается направление движения с учетом направления положения вектора.

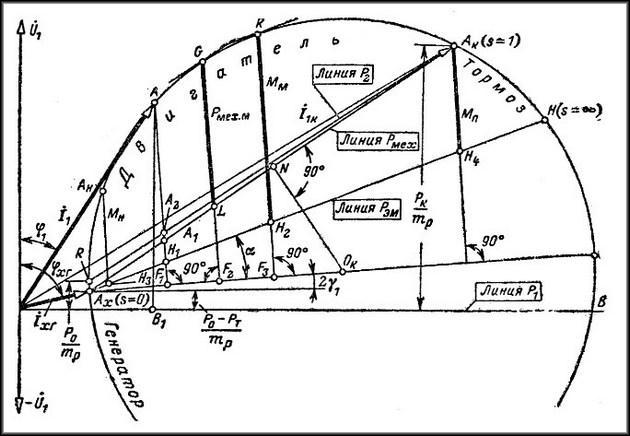
- Линейным. Такой векторной диаграмме при изменении характеристик направление изменяется строго прямолинейно.
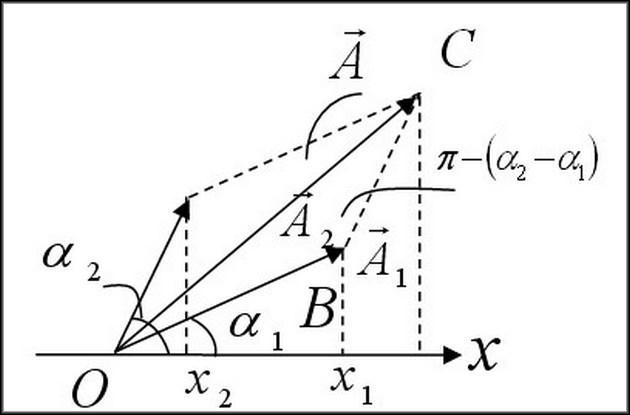

Оба построения могут использоваться для расчета характеристик переменного тока в цепи с сопротивлением и индуктивностью.
Виды и построение векторных диаграмм
Векторные диаграммы широко применяются в акустике, электротехнике, оптике и других областях. Они разделяются на два основных вида – точные и качественные.
Для изображения точных векторных диаграмм применяются численные расчеты с условием, что действующие значения будут соответствовать определенным масштабам. Правильное построение дает возможность геометрического определения фаз и амплитудных значений нужных величин.
Для того чтобы сделать построение диаграмм более удобным, необходимо проанализировать состояние неподвижных векторов на определенный момент времени, выбираемый с таким условием, чтобы сама диаграмма приобрела наиболее оптимальный внешний вид.
На оси ОХ будут откладываться действительные числа, а на оси OY – мнимые числа или единицы. С помощью синусоиды отображается движущийся конец проекции на ось OY. Каждое значение напряжения и тока отображается на плоскости в полярных координатах, в соответствии с собственным вектором. Его длина будет отображать значение амплитудной величины тока, а углы будут равны фазам. Для векторов, отображаемых на диаграмме, характерна равновеликая угловая частота, обозначаемая символом ω. Поэтому во время вращения взаимное расположение угловых частот остается неизменным. Это дает возможность при построении диаграмм направить один вектор произвольно, а остальные отобразить по отношению к нему под различными углами в соответствии со сдвигами фаз.
Диаграммы ВАФ
|
Описание: Данное приложение предназначено для удобного построения векторных диаграмм по результатам измерений во вторичных цепях счетчиков электрической энергии с помощью вольтамперфазометра ПАРМА ВАФ-А или его предыдущих аналогов (ВАФ-85-М1). Простой и удобный инструмент для специалистов, инженеров подразделений учета электроэнергии, служб релейной защиты и автоматики в электросетевых предприятиях, энергосбытовых компаниях, управляющих компаний в сфере ЖКХ. Приложение совместимо со смартфонами и планшетами и выполняет следующие функции:
Инструкция пользователяПосле запуска приложения, нажмите кнопку «Ввод данных», в диалоговом окне приложения пользователю доступно внесение до 3 групп векторов – 1 опорный вектор напряжение/тока + 3 измеренных вектора тока/напряжения с углами, нагрузкой L/C, собственным обозначением. Укажите наименование фидера, например «ПС Заводская Ф.1 Uab», выберите тип опорного вектора – ток или напряжение, введите значение. Для вектора опорного напряжения укажите его тип с помощью переключателя «Лин/Фаз». При необходимости, введите обозначение опорного вектора, в противном случае приложение присвоит обозначение автоматически по шаблону: Uоп№1, либо Iоп№1, где №1 – номер 1-ой группы векторов. С помощью переключателя I/U укажите тип измеренных векторов, для напряжений – с помощью переключателя выберите линейное/фазное. Эти 2 переключателя созданы для автоматического определения обозначений векторов по типу Ia№1/Ua№1/Uab№1 и т.д. На алгоритм построения векторной диаграммы положение указанных переключателей не влияет. Введите значения измеренных токов/напряжений для соответствующих фаз с углами нагрузки, используя переключатель «L/C». Токи/напряжения можно задавать в любых единицах – мА/А/мВ/В, масштаб для векторной диаграммы приложение подбирает автоматически. При необходимости, для каждого вектора задайте собственное обозначение. При его наличии приложение сохранит в базе данных обозначение вектора вместо шаблонного Ia№1/Ua№1/Uab№1. Для удобства пользователя применена цветовая подсветка зон в соответствии с Правилами устройств электроустановок. Нажмите кнопку «Сохранить». Приложение выдаст сообщение «Группа №1. Запись сохранена в БД». Для внесения векторов в группу №2 нажмите на кнопку «Добавить группу I,U». В желтом поле отобразится наименование последнего введенного фидера и приложение перейдет в режим внесения данных для группы векторов №2. Порядок внесения опорного вектора и измеренных векторов одинаковый, как и для группы №1. После завершения внесения данных нажмите кнопку «Сохранить» — приложение выдаст сообщение «Группа №2. Запись сохранена в БД». Для внесения векторов в группу №3 нажмите на кнопку «Добавить группу I,U» и повторите необходимые действия. Нажатием кнопки «Сохранить» данные будут записаны в БД. Использование всех 3 групп не является обязательным – каждая запись в БД может хранить 1, 2 или 3 группы векторов. По кнопке «Просмотр» доступна для просмотра последняя внесенная в базу данных векторная диаграмма. Вектора равные 0 (нулю) приложение заносит в базу данных, но не выводит при просмотре. При нажатии на кнопку «Просмотр данных» приложение перейдет к отображению на экране Вашего устройства последней векторной диаграммы из базы данных. Касанием по указательной стрелке любого из построенных векторов на экран выводится информация о модуле данного вектора и его угле нагрузки. Для суммарных векторов выводится угол, измеряемый от оси «+j» с положительным направлением против часовой стрелки. Просмотр других векторных диаграмм доступен в режиме пролистывания, нажимая кнопки «>». При нажатии кнопки «Удалить» приложение запросит подтверждение на выполнение операции удаления векторной диаграммы из базы данных. При нажатии кнопки «Ред.» приложение переходит в режим редактирования данных векторной диаграммы. Для выбранной в режиме просмотра векторной диаграммы приложение перейдет в редактирование векторов для группы №1. После внесения необходимых изменений нажмите на кнопку «Сохранить». Приложение выдаст сообщение «Группа №1. Запись сохранена в БД». Пользователю доступны те же самые поля и переключатели, что и при первоначальном занесении данных в БД. Для редактирования данных из группы №2 и №3 нажмите соответствующие кнопки. Для сохранения изменений редактирование должно завершаться нажатием кнопки «Сохранить». Сохраненные в базе данных векторные диаграммы можно экспортировать в растровый формат PNG, векторный формат SVG, либо в таблицу Microsoft XML. Для перехода в выбор режима экспорта в главном окне нажмите кнопку «Экспорт данных». Для форматов PNG и SVG укажите размер изображения в пикселях из выпадающего списка «Размер», укажите «Ориентацию» через переключатель «Альбомная/Книжная», далее нажмите кнопку «PNG», либо «SVG». Экспорт в векторный формат является наиболее предпочтительным – создаются векторные файлы небольшого размера, удобные для редактирования. При экспорте в растровый формат приложение создает временные несжатые растровые объекты Bitmap большого размера – от 1,5 до 55 Мбайт на одну векторную диаграмму, и при большом разрешении 3840×2880, 5120×2880 приложение может вызывать ошибку в работе. Для экспорта в таблицу XML нажмите кнопку «XML». В открывшемся окне «Диаграммы БД» выберите необходимые диаграммы из базы данных и нажмите кнопку «Экспорт». После завершения операции приложение выдаст сообщение «Экспорт данных завершен». Все экспортируемые файлы сохраняются в новой папке «MyDiagrams», которая находится в корне устройства «mnt/sdcard». Для удобной и функциональной работы с приложением, пользователю доступны настройки, сохраняемые в памяти Вашего смартфона/планшета: Отображение меток осей координат, круговой сетки, легенды, метки векторов. Режим единого цвета для векторов в группе. Необходимость построения суммарных векторов измеренных величин в различных группах. Необходимость построения опорных векторов. Отображение углов между опорным и измеренным вектором. Режим «Тонкие линии» . Все указанные настройки применяются при выводе на экран в режиме «Просмотр данных», а также в режиме «Экспорт данных» в форматы PNG и SVG. Легенда при просмотре на экране Вашего устройства не отображается, но отображается при экспорте. Как указывалось ранее в разделе «Экспорт данных» возможно завершение работы приложения с ошибкой экспорте в PNG формат векторных диаграмм при большом разрешении 3840×2880, 5120×2880. При необходимости оперативного получения PNG файлов с Вашего устройства и возникновении ошибки, рекомендуется снизить разрешение файлов до 848×480, 1280×720, 1920×1080 точек. Для исключения ошибок при экспорте в графические форматы рекомендуется использовать векторный формат SVG – выходной файл не будет превышать размер 50 Кбайт. Данный формат широко поддерживается следующими программами: браузеры Internet Explorer 9+, Mozilla Firefox 1.5+, Netscape Navigator 9.0+, Google Chrome 3.0+, Safari 4.0+, Opera 8.0+, редакторы Inkscape, LibreOffice Draw, OpenOffice.org Draw, Microsoft Office Visio, sK1 (ОС Linux), Sketch (OSX), Adobe Illustrator, CorelDRAW. Полученные векторные файлы протестированы в браузерах Internet Explorer, Firefox, редакторе Inkscape, а также импортированы с конвертацией в растровое изображение в графический редактор GIMP – векторные диаграммы построены одинаково. Бесплатный редактор LibreOffice Draw неправильно отображает текст метки векторов, так что рекомендуется использовать редактор Inkscape При построении векторных диаграмм приложение размещает метки у векторов на оси вектора близи указательной стрелки. На практике, другие вектора могут перекрывать данные метки. Данная особенность является упрощением в приложении – для перемещения меток векторов используйте векторный формат SVG, в котором перемещение меток в удобное положение реализуется простыми приемами редактирования. Лицензия: Freeware Системные требования: Android 2.3.3 и выше Скриншоты: Скачать APK файл Дополнительные скриншоты: Версия 1.1: 1. Добавлена поддержка 3-х групп векторов – 1 опорный + 3 измеренных вектора. 2. Добавлены переключатели выбора типа опорного вектора – напряжение/ток, переключатель типа измеренных векторов – ток/напряжение (фазное, линейное). 3. Добавлены обозначения всех векторов в 3-х группах. 4. Добавлен режим редактирования векторов во всех 3-х группах 5. Добавлены размеры для экспорта в PNG и SVG форматы — 3840×2880, 5120×2880 точек. 6. Добавлено отображение меток осей координат, круговой сетки, легенды, метки векторов. 7. Добавлен режим единого цвета для векторов в группе. 8. Добавлено вычисление и сохранение суммарных векторов измеренных величин в различных группах. 9. Добавлено отображение углов между опорным и измеренным вектором. 10. Добавлен режим «Тонкие линии». 11. Добавлены «Настройки» приложения. 12. Улучшена стабильность при экспорте в растровый формат PNG. 13. Исправлена ошибка прорисовки экрана при удалении первой векторной диаграммы из БД. 14. Исправлена цветовая схема командных кнопок интерфейса. 15. Исправлена ошибка выбора нагрузки L/C. 16. Исправлена цветовая схема векторов на диаграммах. 17. Исправлен способ именования выходных файлов при экспорте в PNG и SVG форматы. О приложении: Среда разработки: Android Studio https://developer.android.com/sdk/index.html Графика: Paint.NET https://www.getpaint.net/ Плагин Selection menu (BoltBait) https://www.boltbait.com/pdn/ Особая благодарность: StartAndroid.ru Developer.AlexanderKlimov.ru Stackoverflow.com Литература: Ковров И.А. Методы инструментального выявления недостоверного учета электрической энергии. ОАО «НТЦ электроэнергетики». 2010, 36 стр. Александр Игнатов |
Обработка данных для построения лучевой диаграммы
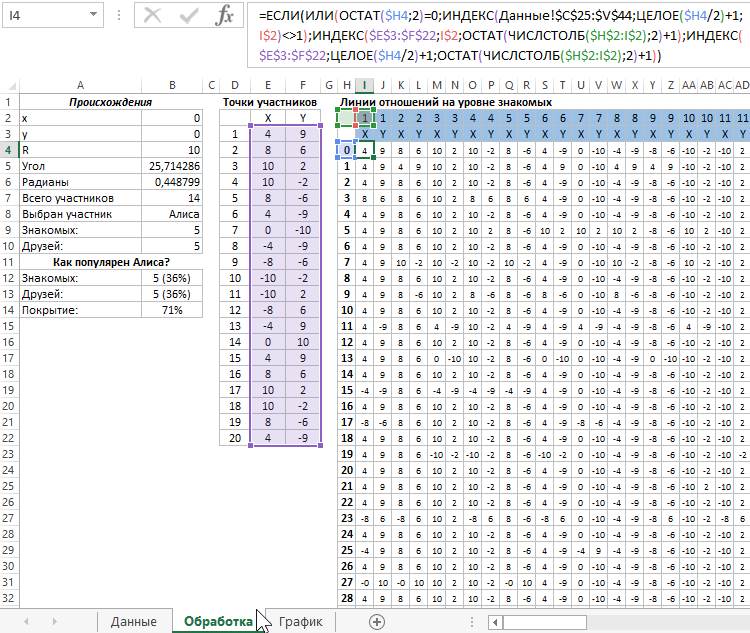
На следующем листе с именем «Обработка» создаем сначала 2 таблицы: одна обычная, вторая умная. Обычная таблица заполнена формулами и значениями так как показано на рисунке:
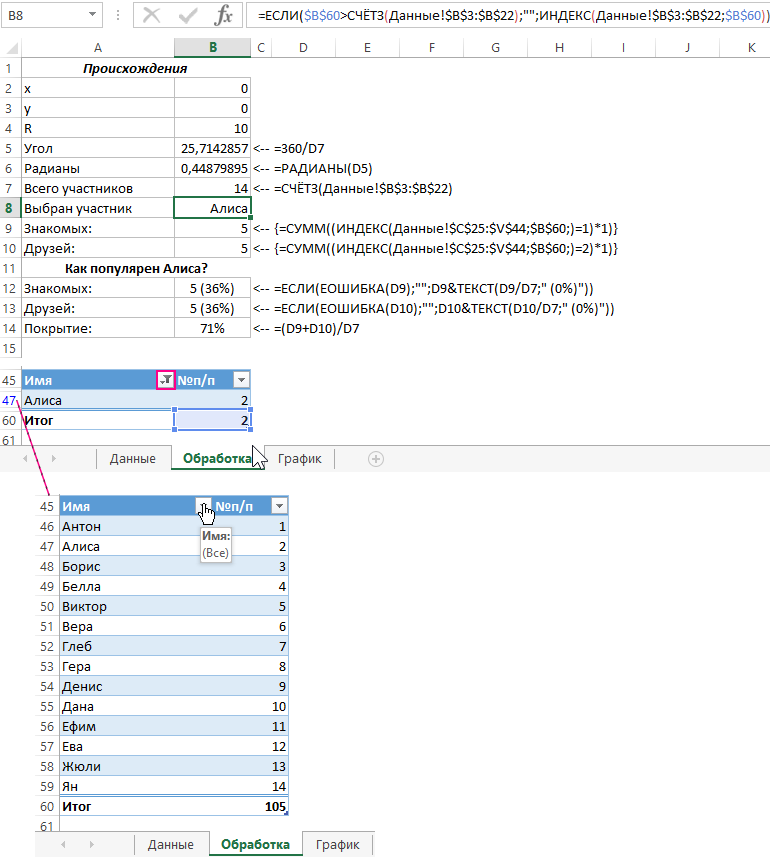

Обратит внимание!!!:
- В ячейках B9 и B10 используются формулы массива поэтому при их вводе следует использовать комбинацию клавиш CTRL+SHIFT+Enter.
- Умная таблица должна быть расположена не выше 45-ой строки текущего листа Excel. Для данной таблице будет регулярно применятся фильтр, который будет скрывать часть строк листа. Нельзя допустить чтобы в эти строки попадали другие значения.
Рядом создаем еще одну таблицу для вычисления координат на основе данных первой таблицы. Для этого используется 2 формулы для значений X и Y:
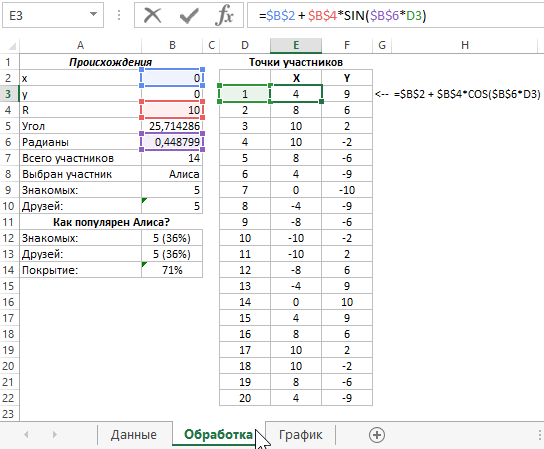

Следующая таблица создана для построения координат линий – отношений на уровне знакомых. Таблица содержит 40 строк и 40 столбцов. Каждая пара столбов – это входящие данные для радов диаграммы. Все ячейки заполнены одной сложной формулой:
Рядом же сразу создаем аналогичным образом таблиц с координатами построения линий – отношений на уровне друзей. Все ее ячейки заполнены формулой:
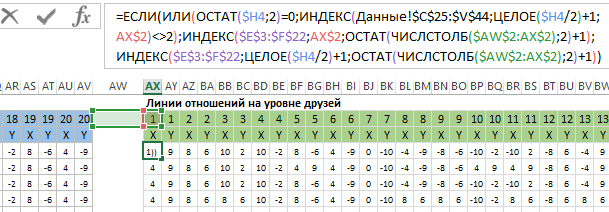

Эти две таблицы будут использованы для построения серых линий. А теперь создадим еще одну таблицу для построения синих и зеленых линий для выделенного участника:
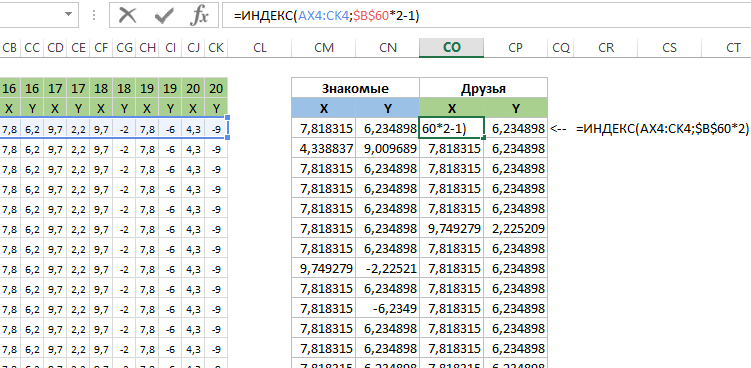

В каждом столбце этой таблицы используются разные формулы:
Столбец листа CM (X-синяя):
CN (Y- синяя):
CO (X- зеленая):
CP (X- зеленая):
Все с обработкой закончили! У нас есть все координаты для точек и линий. Осталось только построить лучевую диаграмму визуализировав таким образом входящие значения на листе «Данные».
Примеры применения
В следующих разделах приведены описания задач, которые решают с помощью представленной методики. Следует подчеркнуть, что применение комплексных чисел пригодно для сложных расчетов с высокой точностью. Однако на практике достаточно часто сравнительно простой векторной графики с наглядным отображением исходной информации на одном рисунке.
Механика, гармонический осциллятор
Таким термином обозначают устройство, которое можно вывести из равновесного состояния. После этого система возвращается в сторону исходного положения, причем сила (F) соответствующего воздействия зависит от дальности первичного перемещения (d) прямо пропорционально. Величину ее можно уточнить с помощью постоянного корректирующего коэффициента (k). Отмеченные определения связаны формулой F=-d*k
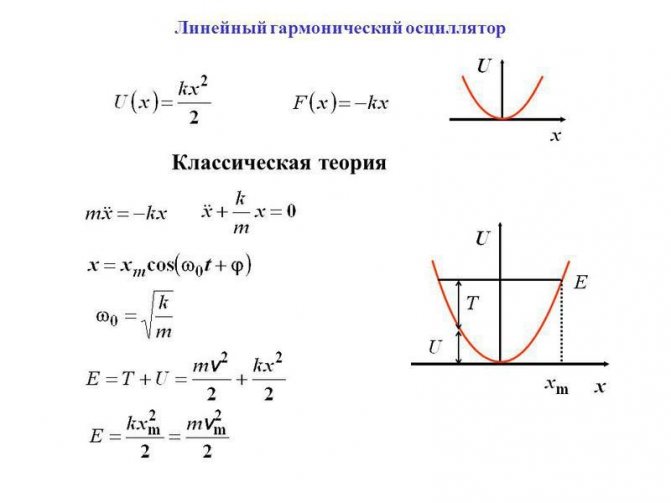

Формулы для расчета основных параметров гармонического осциллятора
К сведению. Аналогичные процессы происходят в системах иной природы. Пример – создание аналога на основе электротехнического колебательного контура (последовательного или параллельного). Формулы остаются теми же с заменой соответствующих параметров.
Свободные гармонические колебания без затухания
Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы. Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.
Гармонический осциллятор с затуханием и внешней вынуждающей силой
В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.
Расчет электрических цепей
Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности. Для более сложных схем пользуются методикой расчета «Комплексных амплитуд», в которой реактивные компоненты определяют с помощью импедансов.
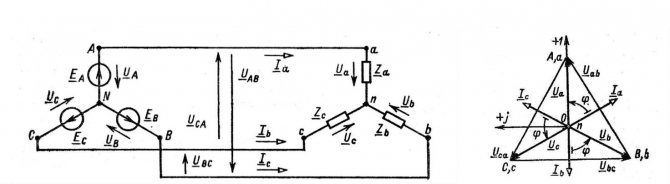

Векторная диаграмма для схемы соединений без нейтрального провода – звезда
Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).
Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.
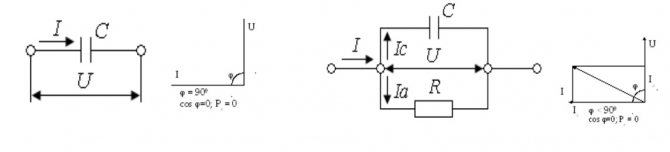

Схемы и векторные диаграммы для идеального элемента и диэлектрика с потерями
Преобразование Фурье
Векторные технологии применяют для анализа спектров радиосигналов в определенном диапазоне. Несмотря на простоту методики, она вполне подходит для получения достаточно точных результатов.
Сложение двух синусоидальных колебаний
В ходе изучения таких источников сигналов рекомендуется работать со сравнительно небольшой разницей частот. Это поможет создать график в удобном для пользователя масштабе.
Фурье-образ прямоугольного сигнала
В этом примере оперируют суммой синусоидальных сигналов. Последовательное сложение векторов образует многоугольник, вращающийся вокруг единой точки. Для правильных расчетов следует учитывать отличия непрерывного и дискретного распределения спектра.
Для этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.
Построение
Построение простых векторных диаграмм будет рассмотрено в данном разделе. Для примера можно взять простую цепь с несколькими элементами и их значениями. Такая схема подразумевает последовательное соединение элементов между собой. Цепь состоит из катушки индуктивности, конденсатора и активного сопротивления. Параметры каждого элемента цепи приведены ниже.
- Катушка индуктивности UL с напряжением 15 вольт. Ток в индуктивном сопротивлении имеет сдвиг фазы 90°.
- Конденсатор UC с напряжением 20 вольт и опережением на 90 градусов.
- Напряжение резистора UR 10 вольт, его направление совпадает с током I.
- Сила тока в цепи I равняется 3 ампера.
Далее можно сделать простую диаграмму, которая поможет определить напряжение для всей схемы.
- Отложить на плоскости I в виде горизонтальной линии с масштабом 1 A/см (масштаб может быть любым, главное — выполнять все элементы диаграммы одного типа в одном масштабе). Сам ток равен 3 ампера, поэтому его длина будет равна 3 см.

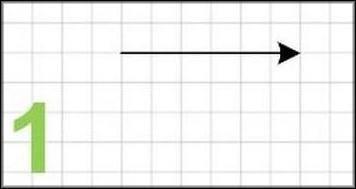
- Теперь необходимо отложить вертикальный вектор UL в масштабе 5 В/см. Он отображает напряжение катушки индуктивности и равен 15 вольт. Его длина на плоскости составит в данном масштабе так же 3 см.

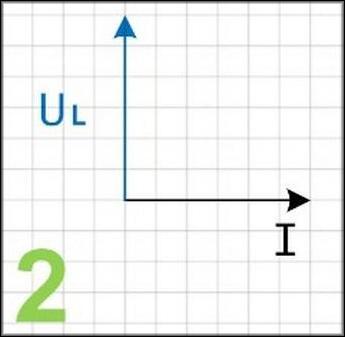
- Далее нужно графически обозначить вектор напряжения активного сопротивления. Его точка отсчета располагается на окончании вертикального вектора UL. Для принятого масштаба 5 В/см ему соответствует вектор длиной 2 см. Линия должна быть строго параллельна горизонтальному вектору I.

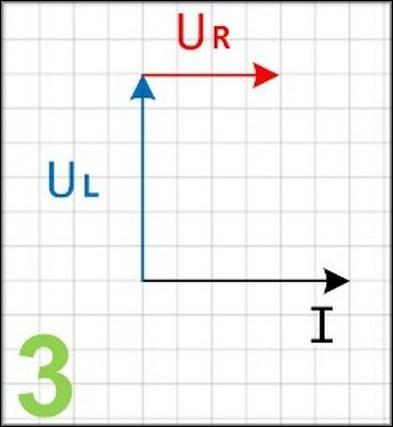
- Теперь нужно отобразить на данной диаграмме напряжение конденсатора UC. Его началом будет конечная точка вектора UR, а конец данного вектора будет расположен ниже горизонтального вектора I. В масштабе 5 В/см ему соответствует вектор длиной 4 см.

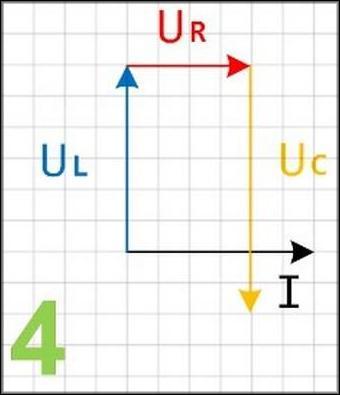
- Чтобы определить соответствующее такой схеме общение напряжение U надо будет сделать следующее. Начало вектора расположено в принятой точке отсчета, а конец его будет расположен в конечной точке вектора UC.
Поэтому если есть схема с последовательным соединением элементов, то всегда можно довольно просто построить векторную диаграмму и рассчитать общее напряжение для такой схемы.
Сложение и вычитание векторов
Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями
Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:
Im = Im1 + Im2
Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.
Вектор Im, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).
Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):
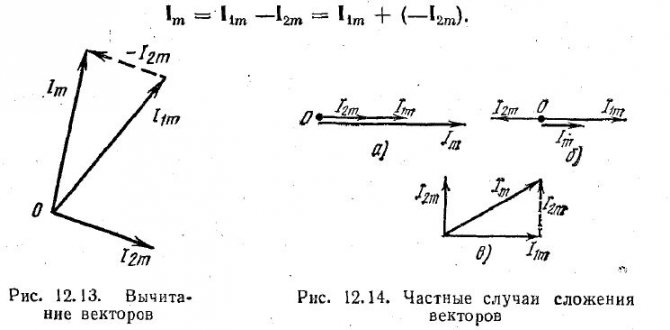

При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.
Векторные диаграммы и комплексное представление
Векторные диаграммы можно считать вариантом (и иллюстрацией) представления колебаний в виде комплексных чисел. При таком сопоставлении ось Ox соответствует оси действительных чисел, а ось Oy – оси чисто мнимых чисел (положительный единичный вектор вдоль которой есть мнимая единица).
Тогда вектор длиной A
, вращающийся в комплексной плоскости с постоянной угловой скоростью
ω
с начальным углом
φ0
запишется как комплексное число
а его действительная часть
-есть гармоническое колебание с циклической частотой ω
и начальной фазой
φ0
.
Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.
- Метод векторных диаграмм может излагаться отдельно в курсах электротехники или элементарной физики, если по тем или иным причинам (обычно связанным с умеренным уровнем математической подготовки учащихся и недостатком времени) надо избежать использования комплексных чисел (в явном виде) вообще.
- Метод комплексного представления (который при необходимости или желании может включать и графическое представление, что, правда, совершенно не обязательно и иногда излишне) вообще говоря более мощен, т.к. естественно включает в себя, например, составление и решение систем уравнений любой сложности, в то время как метод векторных диаграмм в чистом виде всё же ограничен задачами, подразумевающим суммирование, которое можно изобразить на одном чертеже.
- Однако метод векторных диаграмм (в чистом виде или в качестве графической составляющей метода комплексного представления) – более нагляден, а значит в некоторых случаях потенциально более надежен (позволяет до некоторой степени избежать грубых случайных ошибок, которые могут встречаться при абстрактных алгебраических вычислениях) и позволяет в некоторых случаях достичь в каком-то смысле более глубокого понимания задачи.
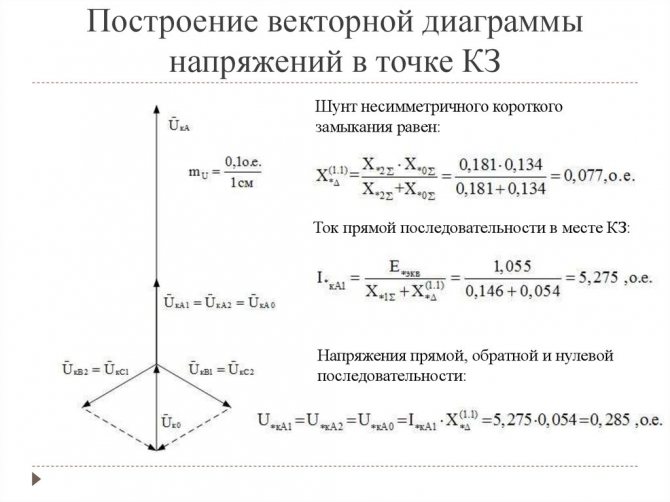
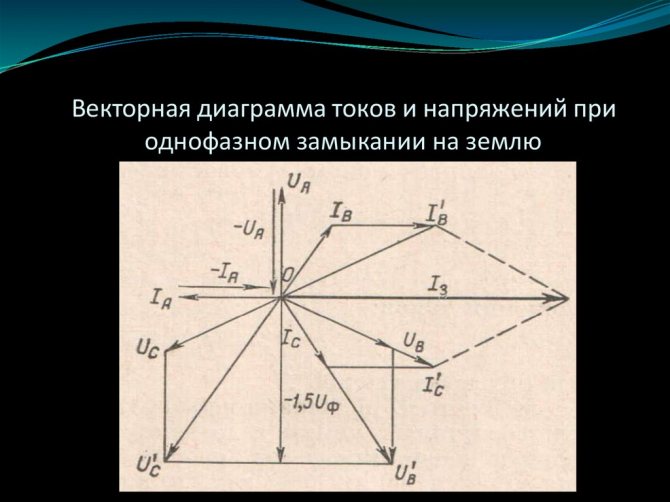
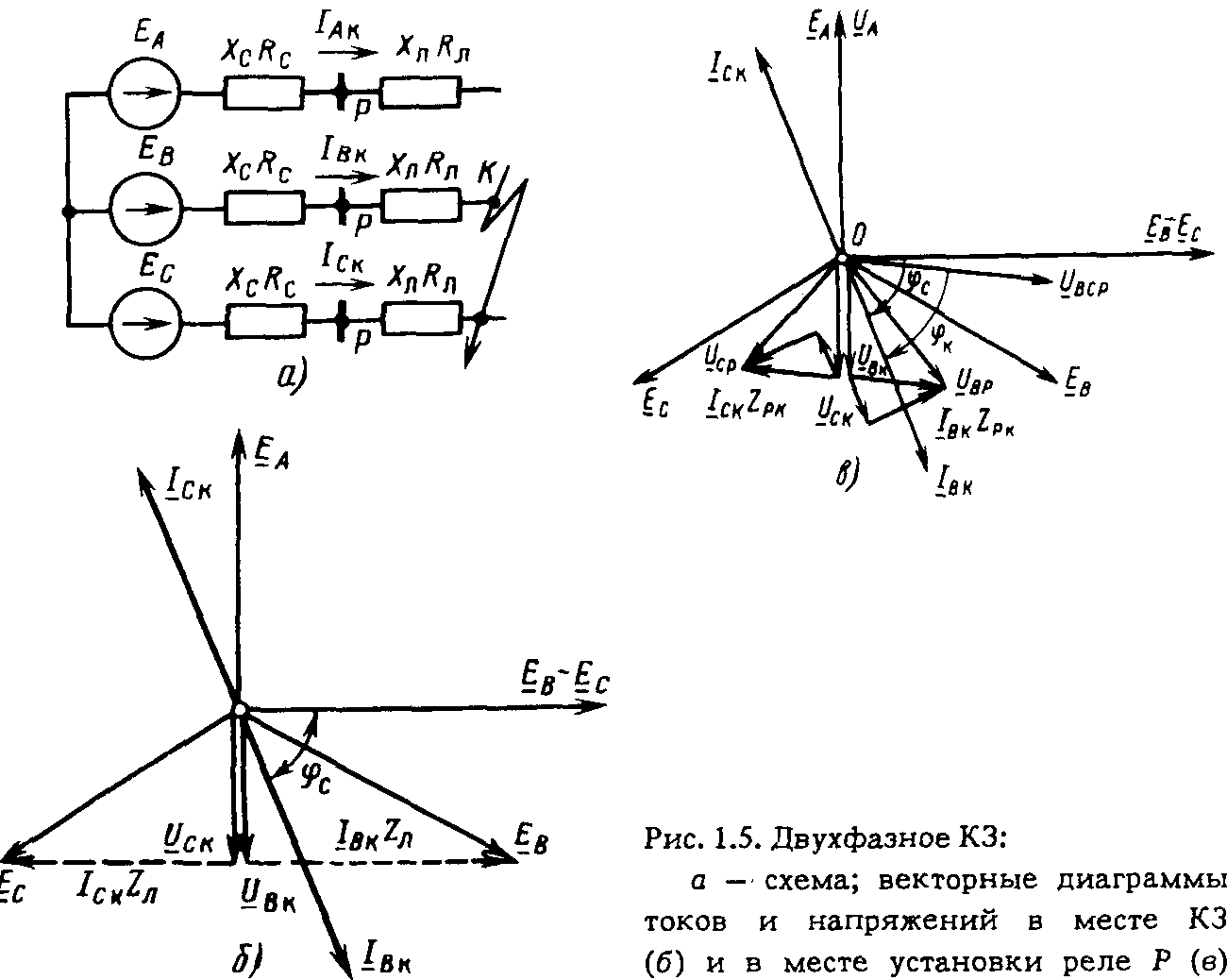
Режим короткого замыкания
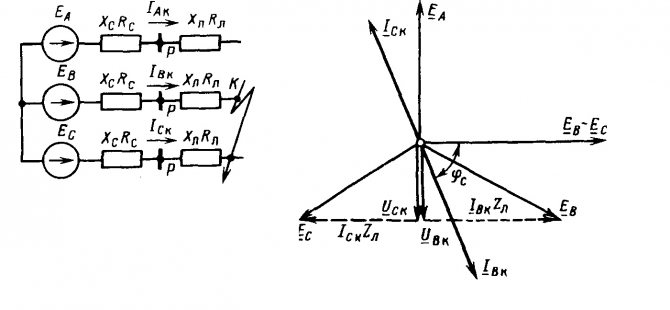
Режимом короткого замыкания называют режим при замкнутой накоротко вторичной обмотке . Схема замещения трансформатора в этом режиме имеет вид, представленный на рис. 11. Для режима короткого замыкания справедливы следующие уравнения:
Векторная диаграмма (рис. 12) в этом режиме строится аналогично векторной диаграмме для режима холостого хода. Угол определяется параметрами вторичной обмотки:. Особенность этого режима состоит в том, что ЭДС значительно отличается от напряжения из-за больших токов короткого замыкания. Учитывая, что , током можно пренебречь. Тогда схема замещения может быть упрощена (рис. 13). Из схемы замещения получаем. Если принять, что , то действующее значение ЭДС будет равно половине действующего значения напряжения :
. Поэтому в режиме короткого замыкания магнитопровод трансформатора оказывается ненасыщенным. Действующее значение тока короткого замыкания в соответствии с рис. 13, где — модуль комплексного сопротивления короткого замыкания трансформатора. При ток короткого замыкания может превосходить номинальное значение в 10-50 раз. Поэтому в условиях эксплуатации режим короткого замыкания является аварийным
Однако этот режим часто проводится при пониженном напряжении для определения параметров трансформатора. Напряжение , при котором ток короткого замыкания равен номинальному, называется напряжением короткого замыкания и обозначается. Отсюда следует, что напряжение короткого замыкания представляет собой падение напряжения на внутреннем сопротивлении трансформатора при номинальном токе и поэтому является важной характеристикой трансформатора
Если совместить вещественную ось с вектором тока , то комплексное значение можно представить как , где , — активная и реактивная составляющие напряжения короткого замыкания. Обычно модуль выражают в относительных единицах,, либо в процентах,. Величина оказывает существенное влияние на свойства трансформатора в рабочих и аварийных режимах. Поэтому является паспортной величиной наряду с номинальными данными.
Потенциальная диаграмма | Электрикам
Потенциальной диаграммой замкнутого контура называется графическая интерпретация распределения электронного потенциала вдоль замкнутого контура в зависимости от входящих в него сопротивлений.
Потребитель энергии отображается на электрической схеме как резистор с заданным сопротивлением R. Если такое элемент присутствует в участке цепи, то изменение потенциалов на концах участка будет соответствовать падению напряжения на этом резисторе.
Если на участке цепи присутствует источник напряжения, то на концах такого участка также будет наблюдаться разность потенциалов, численно равная ЭДС источника.
Построение потенциальной диаграммы
Для построения потенциальной диаграммы, замкнутый контур разбивается на участки таким образом, чтобы каждый из них содержал только одного потребителя или один источник электроэнергии.
Потенциальная диаграмма строится в декартовой системе координат, где по оси абсцисс откладывается, с соблюдением масштаба, сопротивление участков цепи, а по оси ординат – потенциалы точек. Точки замкнутого контура и сопротивления элементов откладываются (отмечаются на диаграмме) в той последовательности, в которой они встречаются при обходе контура.
В начало координат диаграммы помещается точка, потенциал которой условно выбран нулевым.
Демонстрацию алгоритма и правил построения потенциальной диаграммы выполним на примере замкнутого контура abcdef (точки a и f совпадают), представленного на рисунке 1. Положительное направление обхода контура – по часовой стрелке. Для расчетов примем:
- Е1 = 2 В, Е2 = 3 В;
- R1 = 1 Ом, R2 = 1 Ом, R3 = 2 Ом;
- I1 = 1 А, I2 = 2 А, I3 = 1 А.
Рис. 1. Схема фрагмента электрической цепи — замкнутого контура
Замкнутый контур разбит на участки, каждый из которых содержит либо источник ЭДС, либо резистор.
Примем нулевым потенциал точки а
Следующая точка согласно выбранному направлению движения – b. На участке ab находится источник ЭДС E1. Так как движение на данном участке происходит от отрицательного полюса источника к положительному (направление обхода контура совпадает со стрелкой источника ЭДС), то значение потенциалы на участке повысится на величину E1:
Следующий рассматриваемый участок – bc. На нем происходит уменьшение потенциала на величину падения напряжения на резисторе R1.
Аналогичные процессы происходят на участках cd и de. Следовательно,
На участке ef находится еще один источник ЭДС E2. Движение по данному участку реализуется от отрицательного полюса к положительному, следовательно потенциал повысится на величину E2
Если направление обхода контура не совпадает с направлением ЭДС, тогда ЭДС записывают со знаком минус
Значения потенциалов в точках а и f совпадают , что подтверждает правильность расчетов.
На основании полученных данных можно построить потенциальную диаграмму (рисунок 2).
Рис. 2. Потенциальная диаграмма
По потенциальной диаграмме легко можно найти разность потенциалов между любыми точками электрической цепи.
Построение векторной диаграммы
Вращая вектор Im‘ против движения часовой стрелки, в прямоугольной системе координат построим график изменения проекции его на вертикальную ось в пределах одного оборота (одного периода). Получим известный уже график синусоидальной функции, соответствующий заданному уравнению.
При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против вращения часовой стрелки, а отрицательные — по ее движению.
В процессе расчета электрической цепи определяется ряд синусоидальных величин. Все их можно изобразить на одном чертеже при помощи вращающихся векторов, привязав к одной паре взаимно перпендикулярных осей.
Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой.
Например, напряжение и ток в электрической цепи выражаются уравнениями:
u = 125 sin(ωt + 30°)
i = 12 sin(ωt — 20°).
Векторная диаграмма такой цепи изображена на рис. 12.11. Если выбрать масштабы напряжения и тока
Mu = 50 В/см; Mi = 4 А/см;
то
Um = Um/Mu = 125/50 = 2,5 см; Im = Im = im/Mi = 12/4 = 3 см.
Векторная диаграмма содержит векторы синусоидальных величин одинаковой частоты, поэтому они вращаются с одинаковой частотой и их взаимное расположение не меняется.
Начало отсчета времени выбирают произвольно, поэтому один из векторов диаграммы можно направить произвольно; остальные же нужно располагать с учетом сдвига фаз по отношению к первому или предыдущему вектору.
Совокупность радиус-векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения, токи и т. д., называется векторной диаграммой.
Векторные диаграммы наглядно иллюстрируют ход решения задачи. При точном построении векторов можно непосредственно из диаграммы определить амплитуды и фазы искомых величин. Приближенное (качественное) построение диаграмм при аналитическом решении служит надежным контролем корректности хода решения и позволяет легко определить квадрант, в котором находятся определяемые векторы.
При построении векторных диаграмм для цепей с последовательным соединением элементов за базовый (отправной) вектор следует принимать вектор тока (см. лекцию № 8), а к нему под соответствующими углами подстраивать векторы напряжений на отдельных элементах. Для цепей с параллельным соединением элементов за базовый (отправной) вектор следует принять вектор напряжения (см. лекцию № 8), ориентируя относительно него векторы токов в параллельных ветвях.
Для наглядного определения величины и фазы напряжения между различными точками электрической цепи удобно использовать топографические диаграммы.
Они представляют собой соединенные соответственно схеме электрической цепи точки на комплексной плоскости, отображающие их потенциалы. На топографической диаграмме, представляющей собой в принципе векторную диаграмму, порядок расположения векторов напряжений строго соответствует порядку расположения элементов в схеме, а вектор падения напряжения на каждом последующем элементе примыкает к концу вектора напряжения на каждом предыдущем элементе.
В качестве примера построим векторную диаграмму токов, а также топографическую диаграмму потенциалов для схемы, расчет которой был приведен в лекции № 5 (см. рис. 1).
Параметры схемы:
При данных параметрах и заданном напряжении на входе схемы найденные значения токов (см. лекцию № 5) равны: ; ; .
При построении векторной диаграммы зададимся масштабами токов и напряжений (см. рис. 2). Векторную диаграмму можно строить, имея запись комплекса в показательной форме, т.е. по значениям модуля и фазы . Однако на практике удобнее проводить построения, используя алгебраическую форму записи, поскольку при этом вещественная и мнимая составляющие комплексной величины непосредственно откладываются на соответствующих осях комплексной плоскости, определяя положение точки на ней.
Построение векторной диаграммы токов осуществляется непосредственно на основании известных значений их комплексов. Для построения топографической диаграммы предварительно осуществим расчет комплексных потенциалов (другой вариант построения топографической диаграммы предполагает расчет комплексов напряжений на элементах цепи с последующим суммированием векторов напряжений вдоль контура непосредственно на комплексной плоскости).
При построении топографической диаграммы обход контуров можно производить по направлению тока или против. Чаще используют второй вариант.
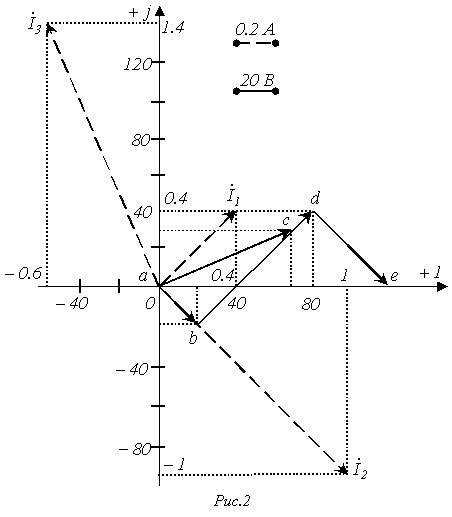

В этом случае с учетом того, что в электротехнике принято, что ток течет от большего потенциала к меньшему, потенциал искомой точки равен потенциалу предыдущей плюс падение напряжения на элементе между этими точками. Если на пути обхода встречается источник ЭДС, то потенциал искомой точки будет равен потенциалу предыдущей плюс величина этой ЭДС, если направление обхода совпадает с направлением ЭДС, и минус величина ЭДС, если не совпадает. Это вытекает из того, что напряжение на источнике ЭДС имеет направление, противоположное ЭДС.
Обозначив на схеме по рис. 1 точки между элементами цепи e и a и приняв потенциал точки а за нуль( ), определим потенциалы этих точек:
или
Таким образом, в результате проведенных вычислений получено, что . Но разность потенциалов точек е
и
а
равно напряжению U, приложенному к цепи, а оно равно 120 В. Таким образом, второй закон Кирхгофа выполняется, а следовательно, вычисления выполнены верно. В соответствии с полученными результатами строится топографическая диаграмма на рис. 2. Следует обратить внимание на ориентацию векторов, составляющих топографическую диаграмму, относительно векторов тока: для резистивных элементов соответствующие векторы параллельны, для индуктивного и емкостных – ортогональны.
В заключение заметим, что векторы напряжений ориентированы относительно точек топографической диаграммы противоположно положительным направлениям напряжений относительно соответствующих точек электрической цепи. В этой связи допускается не указывать на топографической диаграмме направления векторов напряжений.
Потенциальная диаграмма
Потенциальная диаграмма применяется при анализе цепей постоянного тока. Она представляет собой график распределения потенциала вдоль участка цепи или контура, при этом по оси абсцисс откладываются сопротивления резистивных элементов, встречающихся на пути обхода ветви или контура, а по оси ординат – потенциалы соответствующих точек. Таким образом, каждой точке рассматриваемого участка или контура соответствует точка на потенциальной диаграмме.
Рассмотрим построение потенциальной диаграммы на примере схемы на рис. 3.
При параметрах схемы ; ; ; ; и токи в ветвях схемы равны: ; ; .
Построим потенциальную диаграмму для контура abcda
.
Для выбора масштаба по оси абсцисс просуммируем сопротивления резисторов вдоль рассматриваемого контура: после чего определим потенциалы точек контура относительно потенциала произвольно выбранной точки a
, потенциал которой принят за нуль:
Таким образом, координаты точек потенциальной диаграммы: а(0;0);b(4;-20); c(4;17); d(7;2)
. С учетом выбранных масштабов на рис. 4 построена потенциальная диаграмма для выбранного контура.
Преобразование линейных электрических схем
Для упрощения расчета и повышения наглядности анализа сложных электрических цепей во многих случаях рационально подвергнуть их предварительному преобразованию. Очевидно, что преобразование должно приводить к упрощению исходной схемы за счет уменьшения числа ее ветвей и (или) узлов. Такое преобразование называется целесообразным.
При этом при любых способах преобразований должно выполняться условие неизменности токов в ветвях участков схемы, не затронутых этими преобразованиями. Из последнего вытекает, что, если преобразованию подвергаются участки цепи, не содержащие источников энергии, то мощности в исходной и эквивалентной схемах одинаковы. Если в преобразуемые участки входят источники энергии, то в общем случае мощности в исходной и преобразованной цепях будут различны.
Рассмотрим наиболее важные случаи преобразования электрических цепей.
1. Преобразование последовательно соединенных элементов
Рассмотрим участок цепи на рис. 5,а. При расчете внешней по отношению к этому участку цепи данную ветвь можно свести к виду на рис. 5,б, где
| (1) |
или
| . | (2) |
При этом при вычислении эквивалентной ЭДС k-я ЭДС берется со знаком “+”, если ее направление совпадает с направлением эквивалентной ЭДС, и “-”, если не совпадает.
2. Преобразование параллельно соединенных ветвей
Пусть имеем схему на рис. 6,а.
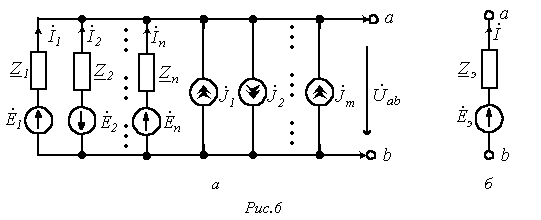

Согласно закону Ома для участка цепи с источником ЭДС
,
где .
Тогда
,
где
| ; | (3) |
| , | (4) |
причем со знаком “+” в (4) записываются ЭДС и ток , если они направлены к тому же узлу, что и ЭДС ; в противном случае они записываются со знаком “-”.
3. Взаимные преобразования “треугольник-звезда”
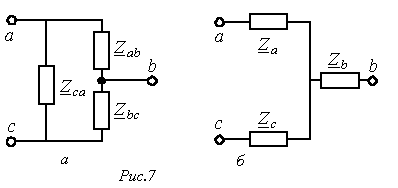

В ряде случаев могут встретиться схемы, соединения в которых нельзя отнести ни к последовательному, ни к параллельному типу (см. рис. 7). В таких случаях преобразования носят более сложный характер: преобразование треугольника в звезду и наоборот.
Преобразовать треугольник в звезду – значит заменить три сопротивления, соединенных в треугольник между какими-то тремя узлами, другими тремя сопротивлениями, соединенными в звезду между теми же точками. При этом на участках схемы, не затронутых этими преобразованиями, токи должны остаться неизменными.
Без вывода запишем формулы эквивалентных преобразований
| Треугольник звезда | Звезда треугольник |
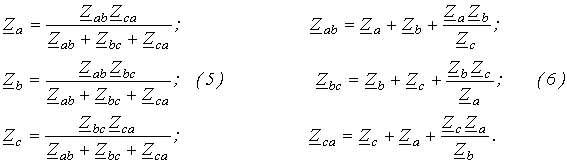
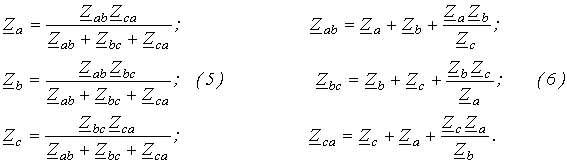
Литература
-
Основы
теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. -
Бессонов Л.А
. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш.шк., 1978. –528с.
Контрольные вопросы и задачи
- Что представляют собой векторные диаграммы?
- Что такое топографические диаграммы, для чего они служат?
- В чем сходство и различие топографической и потенциальной диаграмм?
- Какой практический смысл преобразований электрических цепей?
- В чем заключается принцип эквивалентности преобразований?
- Построить потенциальные диаграммы для левого и внешнего контуров цепи рис.3.
- Полагая в цепи на рис. 8 известными ток и параметры всех ее элементов, качественно построить векторную диаграмму токов и топографическую диаграмму потенциалов для нее.
- Определить входное сопротивление цепи на рис. 8, если .
- Определить сопротивления ветвей треугольника, эквивалентного звезде между узлами a,c и d в цепи на рис. 8.
- Определить сопротивления ветвей звезды, эквивалентной треугольнику в цепи на рис. 8, состоящему из элементов , и .
Ответ: .
Ответ: ; ; .
Ответ: ; ; .
Интерактивная панель управления лучевой диаграммой связей
Для создания панели управления будем использовать обычный срез для уже созданной умной таблицы. Перейдите на любую ячейку умной таблице на листе «Обработка» и выберите инструмент: «ВСТАВКА»-«Фильтры»-«Срез». В паявшемся окне укажите галочкой только на опцию «Имя».
Копируем срез и лучевую диаграмму на отельный лист «ГРАФИК» и наслаждаемся готовым результатом:
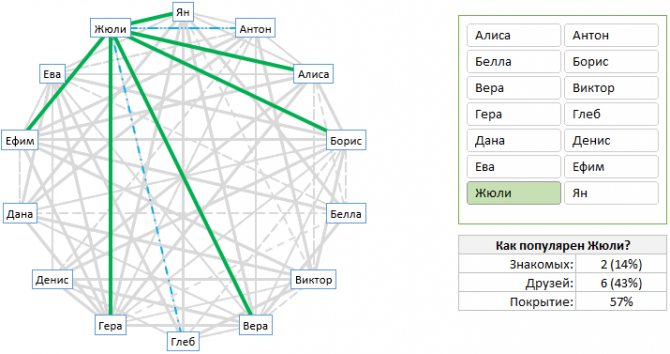

Как видно выше на рисунке было создано всего 43 ряда для лучевой диаграммы связей взаимоотношений участников рынка. Для добавления большого количества рядов на график можно создать макросы, в данном случае можно все седлать вручную.
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
- Теория линейных электрических цепей ТЛЭЦ — Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте — Контрольная работа №1
- — Контрольная работа №2
- — Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил — Контрольная работа № 1 Электрические цепи
- — Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
- Теория линейных электрических цепей ТЛЭЦ — Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте — Контрольная работа №1
- — Контрольная работа №2
- — Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил — Контрольная работа № 1 Электрические цепи
- — Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009
Визуализация данных связей участников на лучевой диаграмме
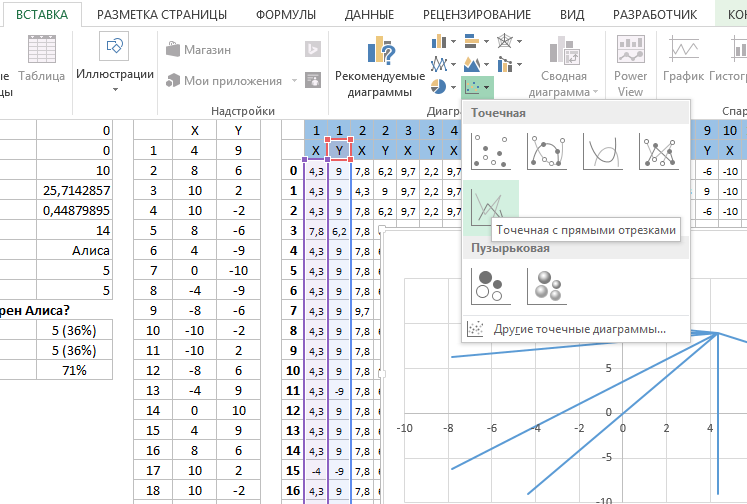
Начнем сначала с построения серых пунктирных линий для отображения всех слабых связей между участниками. А потом сделаем те же самые действия для серых сплошных линий сильных связей. Выделите диапазон ячеек I3:J43 и выберите инструмент: «ВСТАВКА»-«Диаграммы»-«Точечная с прямыми отрезками».
Из диаграммы следует удалить: сетку, оси координат, название и легенду.
Затем из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«КОНСТРУКТОР»-«Выбрать данные» в окне «Выбор источника данных» используйте кнопку «Добавить» для добавления остальных 20-ти рядов:
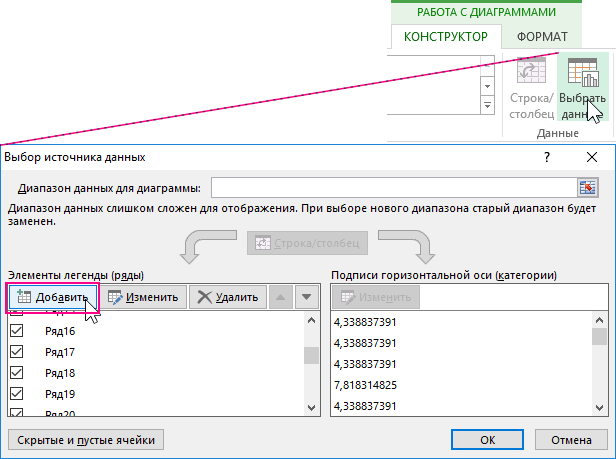

Для каждой линии нужно присвоить один и тот же формат. Удобно выбирать ряды линий из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«ФОРМАТ»-«Текущий фрагмент». Из выпадающего списка выбираем необходимый нам ряд, а ниже жмем кнопку «Формат выделенного» чтобы приступить к форматированию:
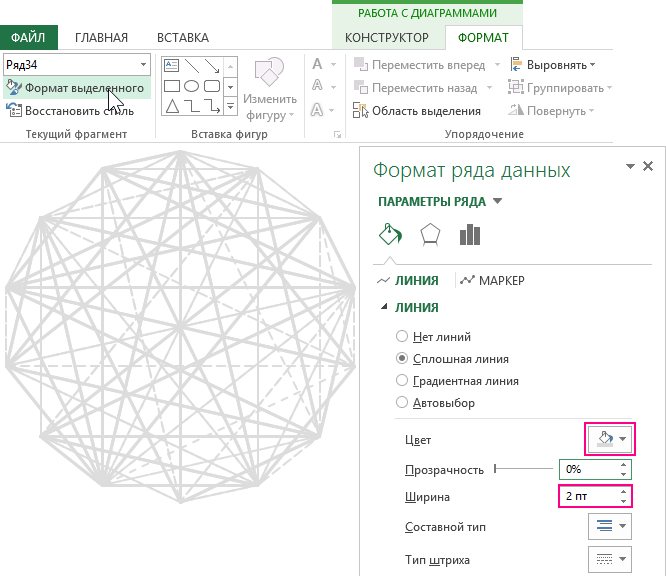

Далее добавляем еще 2 ряда для выделения цветом выбранных участников. Для этого используем значения последней таблицы:
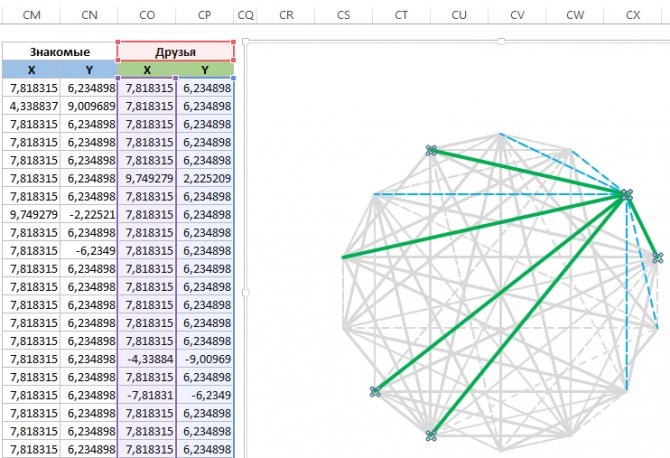

Не забудем изменить цвета линий на зеленый и синий – соответственно.
Осталось еще добавить подписи данных. Для этого используем вторую таблицу с базовыми координатами точек участников при создании еще одного ряда:


Выделяем последний ряд, щелкаем по полюсу возле диаграммы и отмечаем галочкой опцию «Подписи данных». Сам ряд лучше скрыть, убрав завивку для его линий.
Заказать решение ТОЭ
- Метрология Электрические измерения
- Пигарев А.Ю. РГЗ по электротехнике и электронике в Multisim
- Теория линейных электрических цепей ТЛЭЦ — Теория линейных электрических цепей железнодорожной автоматики, телемеханики и связи: задание на контрольные работы № 1 и 2 с методическими указаниями для студентов IV курса специальности Автоматика, телемеханика и связь на железнодорожном транспорте — Контрольная работа №1
- — Контрольная работа №2
- — Электротехника и основы электроники: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей высших учебных заведений / Соколов Б.П., Соколов В.Б. – М.: Высш. шк., 1985. – 128 с, ил — Контрольная работа № 1 Электрические цепи
- — Артеменко Ю.П., Сапожникова Н.М. Теоретические основы электротехники: Пособие по выполнению курсовой работы МГТУ ГА 2009